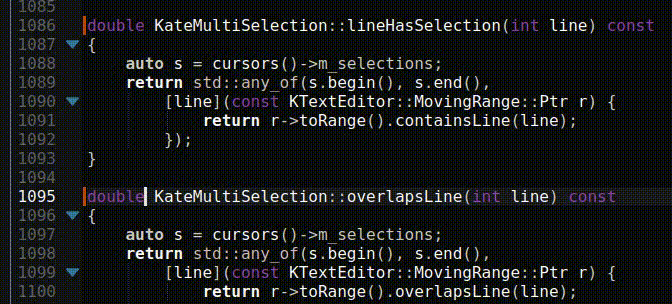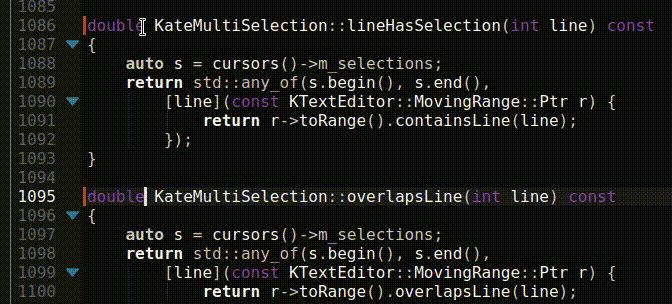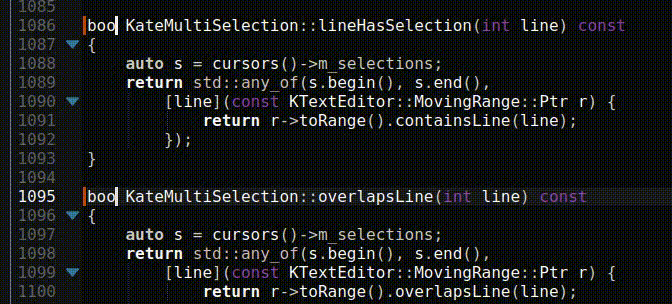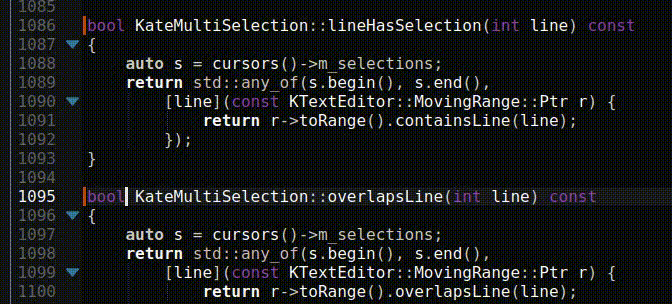
Fourier Transform Spectroscopy continued, or: How to reproduce NIST ASD results to 8+ digits at home

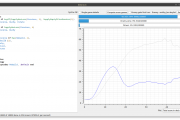
The Atomic Spectra Database (ASD) from the US National Institute of Standards and Technology is a well known tool which contains a large amount of precisely measured electronic transitions in atoms, i.e. spectral lines. Its data is a reference for many fields in science. So, is it possible to build a spectrometer at home which reproduces their accuracy?